Exploring the multifaceted roles of mathematics learning in predicting students' computational thinking competency

Abstract

Background

There exist shared competencies between computational thinking (CT) and mathematics, and these two domains also mutually benefit from various teaching approaches. However, the linkages between mathematics and computational thinking lack robust empirical support, particularly from student-centered learning perspectives. Our study aimed to enhance our understanding of the connections between students' mathematics learning and computational thinking. To assess students' mathematics learning, we measured their beliefs about mathematics learning and their level of mathematical literacy (ML). Our hypothesis posited that students' beliefs concerning mathematics learning, encompassing their views on the nature of mathematics and their attitude towards the subject, can both directly and indirectly influence their CT, with ML serving as a mediating factor. Our data were gathered through surveys and tests administered to eighth- and ninth-grade students. Data were analyzed using partial least squares–structural equation modeling (PLS–SEM).

Results

The evaluation of the measurement model indicated strong internal consistency for each construct. Both convergent and discriminant validity were also established. Upon assessing the structural model, it was found that beliefs about the nature of mathematics positively predicted attitudes towards mathematics, and this belief also indirectly predicted ML through positive attitudes towards mathematics. In addition, ML directly and positively predicted both CT subscales. Notably, a comprehensive mediating effect of ML on beliefs about mathematics learning and CT was identified in the analysis.

Conclusions

This study advances the understanding of the relationships between mathematics learning and CT. We have further confirmed the importance of mathematical literacy in predicting CT and its mediating role between beliefs about mathematics learning and CT. It is suggested that teachers could promote students’ CT competence by enhancing their mathematical literacy or integrating mathematics and CT into the same learning activities. Finally, we propose that upcoming investigations treat CT assessments as formative constructs, diverging from their reflective counterparts.

Introduction

Computational thinking (CT) is a widely applicable form of literacy in the twenty-first century that is necessary for solving problems in various domains (Çoban & Korkmaz, 2021; Grover & Pea, 2018; Peel et al., 2022). The importance of providing students with CT-integrated education has been gaining global attention, and the presence of CT in K-12 classrooms has also been increasing over the last decade (Hurt et al., 2023; Lee & Lee, 2021; Shute et al., 2017; Weintrop et al., 2021; Ye et al., 2023). CT is regarded as a series of thinking abilities that use fundamental concepts of computer science to solve problems (Wing, 2006). It integrates mathematical thinking, engineering thinking and scientific thinking in solving problems, designing and evaluating systems, and understanding intelligence and human behavior (Wing, 2008). Researchers have also claimed that CT should be considered as a domain-general ability, that is, the ability to solve complex daily-life problems (Li et al., 2020b; Yadav et al., 2016). In other words, CT involves solving problems using the abilities to order logically, analyze data, and create solutions by following sequences and rules. It also allows students to apply what they have learned in real-life situations (Yadav et al., 2016).

Recent literature provides valuable insights into the intricate interplay between CT and mathematics education, as well as the connection between CT and mathematical thinking (MT). From a competency perspective, CT and mathematics share common competencies, such as problem solving, modeling, analyzing and interpreting data, statistics and probability (Sneider et al., 2014). Mathematics thinking and computational thinking are similar in terms of abstract problem solving, and they may support each other (Rycroft-Smith & Connolly, 2019). Researchers have also claimed that the process of mathematical problem solving involves components of CT (Denning, 2017; Nurhayati & Lutfianto, 2020).

From a teaching perspective, mathematical activities can be used as a starting point for CT (Kallia et al., 2021), and CT and mathematics learning objectives can be integrated into the same curriculum (Chan et al., 2023; Pei et al., 2018). Through a systemic literature review, Khoo et al. (2022) found that CT was implemented into mathematics education through two common approaches, namely, using software tools as a medium for CT in the mathematics curriculum, and teaching CT as a way of thinking. The former approach was also commonly used in engineering and STEM, where computing skills and computer programming were taught using CT in relation to mathematics (Ersozlu et al., 2023). In another study, Wu and Yang (2022) reviewed how CT and MT have been integrated into mathematics education. They concluded three types of relationships between CT and MT, namely: (1) contribution of CT to MT, usually when using software and programming; (2) contribution of MT to CT in problem solving, and (3) reciprocal relationships between CT and MT through embedding CT into mathematics education.

Although the aforementioned studies have classified the relationships between mathematics and CT from teaching perspectives, empirical evidence from learners' perspectives and competence in this area remains limited. Moreover, while past studies have been using qualitative methods to explore the relationships between mathematics and CT teaching, there is a lack of statistical models that accurately depict the direct and indirect relationships among constructs related to mathematics learning and CT (Lv et al., 2023). Thus, our study aimed to gain insights into the associations between students’ mathematical learning and CT through quantitative modeling. In our model, we specifically include beliefs about learning mathematics as a crucial component. Learners' beliefs about, attitude towards, and perceptions of mathematics can significantly influence their engagement in, motivation for, and approach to mathematical learning (Gjicali & Lipnevich, 2021; Metzger et al., 2019). To adopt a competency-focused perspective and to emphasize the real-life applicability of mathematics and computational thinking, we chose to measure two key constructs: mathematical literacy and non-programming CT competence.

The Organization for Economic Cooperation and Development (OECD, ) defines mathematical literacy as the ability to engage with and use mathematics in various contexts, effectively applying mathematical concepts, reasoning, and problem-solving skills to solve real-life problems. It encompasses the capacity to understand, interpret, and critically evaluate mathematical information. Non-programming CT competence refers to the ability to think critically and algorithmically, solve problems, analyze data, and make informed decisions using computational thinking strategies that do not require programming (Selby & Woollard, 2013; Shute et al., 2017). Further details about our hypothesized model will be provided later, offering a more comprehensive explanation.

Computational thinking (CT)

Researchers have provided various definitions of CT. On one hand, CT has been described as being related to computer programming and computer concepts. For instance, CT has been defined as identifying computational aspects of the world and applying computer science tools and methodologies to comprehend the functioning of natural and man-made systems (Royal Society, 2012). Brennan and Resnick (2012) have specifically defined three key dimensions of CT: computational concepts, computational practices, and computational perspectives. Looking through a data modeling lens, Weintrop et al. (2016) classified CT into four categories, namely, data practices, modeling and simulation, computational problem solving, and systems thinking. In sum, the programming-related CT definitions are diverse and focus on different aspects of computing or programming.

On the other hand, CT has been recognized as a fundamental competence for general problem solving and as a cognitive process rooted in logical reasoning (Csizmadia et al., 2015; Tang et al., 2020). Many definitions encompass algorithmic thinking, decomposition, pattern generalization, abstractions, and evaluation, which can be effectively utilized for curriculum development and assessment (Csizmadia et al., 2015; Selby & Woollard, 2013; Shute et al., 2017). According to Csizmadia et al.'s (2015) suggested CT definitions, algorithmic thinking refers to the capability to discern sequences and rules to address issues or understand scenarios. Decomposition involves the ability to break down problems into components, while generalization is the ability for solving problems rapidly based on previous solutions. In addition, abstraction denotes the skill to eliminate unnecessary details for making problem solving more feasible and effective. Finally, evaluation pertains to the capacity to ascertain if a solution, whether an algorithm, system, or process, is suitable for its intended purpose. In our study, we adopted the CT definition aligned with the problem-solving perspective and assessed students' thinking skills in real-life situations (Selby & Woollard, 2013; Shute et al., 2017).

Scholars have developed different assessment tools based on the aforementioned definitions of CT, and the assessment tools for CT are categorized into self-reported CT scales and CT tests (Cutumisu et al., 2019). An instance of a CT scale is the Computational Thinking Scale (CTS) devised by Korkmaz et al. (2017), comprising subscales, such as algorithmic thinking, creativity, cooperativity, critical thinking, and problem solving. CT tests could be further categorized into two subtypes: domain-specific CT assessment, such as programming-based or computer concept-based CT assessment, and domain-general CT assessment. An illustration of a domain-specific assessment is the computational thinking test (CTT), a programming-based CT assessment introduced by Román-González et al. (2018a). It was designed to assess middle school students’ CT skills through computer science concepts, such as sequences and loops. A sample question asks students which code makes the correct path that takes Pac-Man to the ghost. An example of domain-general CT assessment is the Bebras® Computing Challenge, an international competition for informatics and computational thinking (https://www.bebras.org/). Bebras aims to foster students’ CT interest and competence by solving problems based on real-life situations. Devoid of any programming involvement, the Bebras challenge aims to evaluate participants' abilities, whether directly or indirectly linked to CT (Dagiene & Stupuriene, 2016). In this study, the CT measurement was derived from Bebras to assess students' proficiency in applying their CT skills to diverse problems and situations (del Olmo-Muñoz et al., 2020).

Mathematical literacy

Researchers have also uncovered the interplay between ML and various psychological factors, including enhanced mathematics self-efficacy, motivation, mathematics intentions, and perseverance (Kitsantas et al., 2021; Ozgen, 2013; Rahmi et al., 2017; Skaalvik et al., 2015). Mathematical Literacy (ML) encompasses a spectrum of attributes, spanning from adept mathematical reasoning and comprehensive content knowledge to a positive mathematical disposition. It further encapsulates an awareness of mathematics' practical utility and an appreciation of the essence and nature of mathematics (Edge, 2009).

Beyond mere proficiency in mathematical knowledge and skills, mathematical literacy (ML) encompasses the adeptness and confidence to apply mathematical insights within real-life contexts (Ojose, 2011). In other words, the significance of mathematical literacy lies in its potential to inspire students to address practical problems rooted in mathematical concepts (Consortium for Mathematics and Its Applications [COMAP], 2015). This imperative is reflected in the assessment of ML within the Programme for International Student Assessment (PISA) test, where it emphasizes the application of mathematics in authentic scenarios. Here, students' capacity for mathematical reasoning and depicting relationships holds more weight than their proficiency in tackling conventional textbook queries, serving as a robust indicator of their mathematical competencies (Lin & Tai, 2015).

In this study, we adopted the ML definitions coined by the Organization for Economic Co-operation and Development (OECD) by which ML is as "an individual's capacity to formulate, employ, and interpret mathematics across a spectrum of situations" (OECD, 2013, p. 25). The term employ refers to the application of accumulated mathematical knowledge, which encompasses principles, methodologies, facts, and tools, to address mathematical challenges. Formulate signifies the ability to identify opportunities for applying mathematics and to transform problems into patterns that align with mathematical structural representations. Interpret refers to the ability to recognize and explain the relationship between mathematical solutions or responses and the contexts of real-world scenarios (OECD, 2019).

Beliefs related to mathematics learning

In the field of cognitive psychology, there has been increasing interest in studying students’ beliefs about mathematics learning (Jin et al., 2010; Leder et al., 2006). Mathematical beliefs refer to the personal opinions, attitude, or values that individuals hold about mathematics and the nature of mathematics (Ernest, 1989; Underhill, 1988). Other researchers have also included students’ perceptions of mathematics usefulness, mathematics learning, and mathematics teaching as constructs of beliefs about mathematics learning (Lazim, 2004; McLeod, 1992). Researchers have found empirical evidence of a relationship between students’ beliefs about the nature of mathematics and their mathematics learning. Students with positive beliefs about and attitude towards mathematics tend to perform better (Papanastasiou, 2000). Studies have shown that beliefs about mathematics learning could positively predict mathematics outcomes, such as performance on mathematics tests (Bonne & Johnston, 2016; House & Telese, 2008; Suthar & Tarmizi, 2010; Suthar et al., 2010). Scholars have suggested that future research could further investigate beliefs about the nature of mathematics and about students’ mathematical capability due to their relationships with students’ mathematics self-efficacy and their mathematics achievements (Yin et al., 2020).

Hypothesized model

In this study, we hypothesized that students’ beliefs about the nature of mathematics and their attitude towards mathematics could both directly and indirectly predict their CT through the mediation of mathematics performance. First, we hypothesized that beliefs about mathematics learning are predictors of ML and CT. These hypotheses have been based on previous studies which found that students’ beliefs may contribute to higher levels of thinking or competencies. As mentioned earlier, studies have shown that beliefs about mathematics learning can positively predict mathematics outcomes (Bonne & Johnston, 2016; House & Telese, 2008; Suthar & Tarmizi, 2010; Suthar et al., 2010). Sanico’s (2019) study demonstrated that mathematics belief was positively correlated with mathematics problem-solving performance, but could only indirectly predict mathematical problem-solving performance. Schommer-Aikins et al. (2005) also discovered that mathematical problem-solving beliefs and epistemological beliefs could positively predict students’ mathematics performance. To date, few studies have explored the relationships between beliefs about mathematics learning and CT. Nevertheless, other beliefs have been found to be predictors of CT. For instance, research has shown that students’ beliefs about computer programming can predict their computational thinking (Lee et al., 2023).

Second, we hypothesized that ML predicts students’ CT. Since our study focused on non-programming CT, we adopted the perspective of the “contribution of mathematical thinking to CT,” as previously mentioned (Wu & Yang, 2022). Studies integrating CT into mathematics education have shown positive results regarding the relationship between CT and mathematics learning outcomes (Sung & Black, 2020; Sung et al., 2017; Suters & Suters, 2020). For instance, Özgür (2020) conducted research on the relationship between CT and students’ previous mathematics academic achievement through structural equation modeling (SEM). The results demonstrated that students’ previous mathematics academic achievement was not only positively correlated with CT, but could also positively predict CT, and the same result was found by Durak and Saritepeci (2018) and Finke et al. (2022). Guggemos (2021) measured CT and mathematical skills at three different timepoints to see the relationships between these two types of skills. The results showed that CT at any timepoint was positively correlated with students’ mathematical skills, and CT was positively predicted by mathematical skills. What is worth mentioning here is that most of the aforementioned studies studied mathematics achievement. Mathematics achievement measures an individual's performance within the confines of a specific curriculum or learning content within a certain period of time (i.e., a semester), while mathematical literacy, as the focus of the current study, goes beyond this and assesses the practical application of mathematics knowledge in real-world contexts. Nevertheless, both concepts are important for overall mathematics proficiency, and are interconnected.

Finally, we hypothesized relationships between the sub-scales of beliefs about mathematics learning and the sub-scales of CT. Our primary interest was to explore potential hierarchical relationships between these two sets of sub-scales. Furthermore, we chose to use first-order rather than second-order constructs as they offer a more straightforward representation of relationships (Hair et al., 2021).

Specifically, we hypothesized that beliefs about nature of mathematics would predict attitude towards mathematics. However, we also acknowledged the possibility of a reciprocal relationship, where the nature of mathematics could also predict attitude towards mathematics. Beliefs about nature of mathematics represents a learner's philosophical orientation towards the nature of knowledge, while attitude towards mathematics reflects self-evaluations of emotions, interest, motivation, and perceived usefulness of the subject. We assume that an epistemic and philosophical construct can serve as a predictor of an affective construct.

In a previous study, Tsai et al. (2022) found that CT dispositions were divided into lower level and higher level based on the level of cognitive complexity and the information-processing theory of human problem solving. Tsai et al. (2022) showed that lower level CT components, such as abstraction and decomposition, significantly predicted higher level CT, including algorithmic thinking, evaluation, and generalization. We aimed to investigate whether a similar pattern exists in the context of CT competence.

In this study, the measurement of CT, the computational thinking test for Junior High Students (CTT–JH) (Lee et al., 2023), was adapted and modified from the Bebras Challenges and was used to determine how well students could apply their CT skills to real-life problems and situations (del Olmo-Muñoz et al., 2020). This instrument focused on a generous process of problem solving which is independent of the type of programming language. In addition, this instrument has been well-validated and has good reliability overall, as well as in all five dimensions based on empirical data (Lee et al., 2023).

In sum, the hypothesized model is shown in Fig. 1. The purposes of this study were (1) to investigate the roles of beliefs about mathematics learning and mathematical literacy in predicting CT competence, and (2) to investigate the mediating role of ML in the proposed model.

Fig. 1

Hypothesized model showing the relationships between beliefs about the nature of mathematics, attitude towards mathematics, mathematical literacy, and computational thinking (lower level and higher level)

Methods

Research instruments

Computational thinking test

We adapted items from the measurement of CT, the computational thinking test for Junior High Students (CTT–JH) (Lee et al., 2023). The test was developed based on Bebras Challenge tasks for assessing five dimensions of CT, namely, abstraction, decomposition, algorithmic thinking, evaluation, and generalization. These five dimensions were defined as the competence of abstracting essential information, breaking down complicated problems into manageable parts, thinking procedurally as a sequence of steps to reach a solution, deciding the most appropriate solution to the problem, and adapting and transferring solutions to other problems (Lee et al., 2023). Each item was designed to assess one or more CT dimensions simultaneously, and collectively CTT–JH is a multi-dimensional research instrument. The assessment comprises multiple-choice questions, with each correct answer earning 1 point. To further categorize the items into lower and higher levels of CT, the first author and two other experts in computing education and CT research reviewed the items. The group of experts examined the CT dimensions assessed by each item and, as a result, four items assessing lower level CT and four assessing higher level CT were selected. Lower level CT primarily assesses abstraction and decomposition, while higher level CT assesses algorithmic thinking, evaluation, and generalization (Tsai et al., 2022). A sample question is shown in Appendix 1. The corresponding CT dimensions for each item are shown in Appendix 2.

Mathematical literacy test

The ML measurement was adapted from the mathematical reasoning items of PISA 2012. A total of nine items were included in the test in this study, with three questions for each of the employ, formulate and interpret constructs. Each item in the assessment consisted of a multiple-choice question, with 1 point awarded for a correct answer. Students’ ability to work out solutions to mathematical problems through applying mathematical concepts (employ), transform problems into mathematical structures (formulate), and determine and explain the connection between mathematical solutions and real-life situations (interpret) were assessed. To further ensure the content validity of the items, the first author and two other experts in mathematics education reviewed and selected the items. Sample questions are shown in Appendix 3.

The beliefs about the nature of mathematics scale and the attitude towards mathematics scale

The items for both the Beliefs about the Nature of Mathematics Scale and the Attitude towards Mathematics Scale were adapted from a questionnaire about beliefs in mathematics (Lazim et al., 2004; Su, 2018). Beliefs about the nature of mathematics refers to students' perspectives on mathematics and its significance in their lives. Attitude towards mathematics encompasses students' holistic evaluation, perception, and emotional stance towards mathematics, encompassing their preferences, confidence, interest, and perceived utility or relevance of mathematics in their daily lives. We made the decision to rename the original “self-evaluation” scale to “attitude towards mathematics” to better capture the essence of the items included in this scale.

The initial questionnaire consisted of five items each for beliefs about the nature of mathematics (NM) and attitude towards mathematics (AM). All items were rated on a 5-point Likert scale, ranging from 1 (strongly disagree) to 5 (strongly agree). For example, an NM sample item is “Mathematics enables people to understand the world better,” while an AM sample item is “I have been performing well in mathematics exams.” During the PLS–SEM analysis, one item from the original set of questions for the NM scale was excluded due to its low factor loading. For a comprehensive list of the remaining items in both scales, please refer to Table 1 in the Results section.

Table 1 Construct reliability and validity

Data collection and data analysis

Participants were recruited from eighth- and ninth-grade students attending four junior high schools in central Taiwan. Data collection took place in both urban and rural areas, with two schools selected from each setting. This approach ensured the inclusion of a more diverse range of socio-economic backgrounds. Out of the 265 students who initially participated in the study, 247 valid samples were retained, comprising 131 females and 116 males. Data were collected using face-to-face paper-and-pencil questionnaires and tests. Prior to administering the survey, the research team obtained oral consent from each participant. This process involved explaining the study's purpose and nature, highlighting voluntary participation, and assuring the confidentiality and anonymity of responses. Participants were assured that their test results would not impact their school grades. Their rights were fully disclosed, and they had the option to decline participation or withdraw at any time without any consequences. The research team also ensured that participants had the opportunity to ask questions and seek clarification before giving their oral consent. Subsequently, the questionnaires and tests were administered consecutively, with the entire process typically taking no more than 90 min to complete.

The decision to employ partial least squares–structural equation modeling (PLS–SEM) instead of covariance-based structural equation modeling (CB–SEM) in this study was driven by several considerations. First, due to the relatively small amount of data, PLS–SEM was deemed more appropriate. Second, PLS–SEM is recognized for its strong predictive capabilities, as it focuses on minimizing residual variance and enabling accurate predictions based on the model (Lin et al., 2020). This aligns well with the study's focus on variables related to mathematics learning that potentially predict CT.

Third, PLS–SEM offers the advantage of accommodating both formative and reflective constructs within the model (Hair et al., 2021). Reflective constructs represent latent variables measured by observed indicators, while formative constructs are composed of observed variables that collectively define the latent variable. Formative constructs are particularly useful when the construct being measured is seen as a combination of different dimensions or factors, with each observed variable contributing uniquely to the construct (Hair et al., 2021). In this study, while beliefs about the nature of mathematics and attitude towards mathematics were treated as reflective constructs, the CT test and ML test were considered as formative constructs. In sum, by utilizing PLS–SEM, this study addressed the limitations posed by the small amount of data, leveraged the predictive capabilities of the model, and accommodated both formative and reflective constructs.

Two-stage evaluation was employed using PLS–SEM: evaluation of the measurement model and evaluation of the structural model. The evaluation criteria for the measurement model (i.e., the first stage evaluation) have to be met before further analyzing the structural model (i.e., the second-stage evaluation). For the measurement model, the reflective constructs were evaluated by assessing the internal consistency reliability, convergent validity, and discriminant validity. The formative constructs were evaluated by assessing variance inflation factor values (VIF), and outer weights. The structural model was then evaluated using the PLS–SEM algorithm and bootstrapping resampling to test the statistical significance of the path coefficients. The path weighting scheme was selected as the weighting method, with a threshold value of 1·10^–5 (i.e., stop criterion), and a value of at least 300 for the maximum number of iterations (Hair et al., 2021). This study applied the bootstrapping procedure with 247 cases and 5000 samples to test the contribution of the formative indicators to their associated constructs and the structural path significance.

To assess the predictive power of the model, several measures were calculated, including the effect size (f²), coefficient of determination (R² value), and Q² value. The R² value quantifies the extent to which the exogenous constructs linked to an endogenous construct explain its variance (Sarstedt et al., 2016). The effect size f², on the other hand, quantifies the magnitude of change in R² when a construct is omitted from the model, offering insights into the influence of one construct on another (Hair et al., 2021). In addition, the Q² value (Geisser, 1974) serves as another measure to assess the internal model, specifically its predictive relevance for a given endogenous construct.

Results

Measurement model

Construct reliabilities and construct validities were tested to examine the quality of the measurement model. Reliability for verifying internal consistency of the indicators of each construct was tested by the composite reliability (CR) values and the Cronbach’s alpha values (Fornell & Larcker, 1981). As shown in Table 1, the CR values of the constructs were 0.82 and 0.93, which were above the suggested value of 0.70. The Cronbach’s alpha values of the constructs were 0.71 and 0.90, which also met the requirement of being greater than 0.70. These results show that the internal consistency of the indicators for each construct was good, and the measurement model had sufficient reliability.

To verify whether the measurements effectively reflected the corresponding measured constructs, convergent validity and discriminant validity were assessed. Convergent validity of the measurements was validated by factor loadings of indicators and the average variance extracted (AVE) of constructs (Hair et al., 2019). The factor loadings of the individual items were all above 0.6 (see Table 1), which is acceptable according to Hair et al. (2021). The AVE values of the constructs were 0.53 and 0.72, which were higher than the suggested value of 0.5. In accordance with Fornell and Larcker (1981), these results suggested adequate convergent validity.

Discriminant validity, which refers to the degree to which each construct in the resulting model is distinct from the others, was measured through the Fornell–Larcker criterion (Fornell & Larcker, 1981) and cross loadings. The cross loadings of measurement variables should be higher than the related latent variable (Chin, 1998). The correlation matrix and the square root of the AVE value of Nature of Mathematics and Attitude towards Mathematics are shown in Table 2. The results showed that the two variables were significantly correlated with each other (r = 0.56, p < 0.001) and the square root of the AVE value of each variable was higher than 0.5 (0.73, 0.85) and larger than the Pearson’s correlation coefficient between the two variables. As shown in Table 3, all cross loadings were higher than each related latent variable. Therefore, the discriminant validity of the variables was confirmed (Hair et al., 2021).

Table 2 Discriminant validity (Fornell–Larcker criterion)

Table 3 Discriminant validity (cross loadings)

In our analysis, the collinearity, significance, and relevance of formative indicators or items within the measurement models were assessed by variance inflation factor (VIF), outer weights, and outer loadings for this analysis. In this research, both CT and ML were considered as formative constructs. Moreover, CT was categorized into lower level (LLCT) and higher level CT (HLCT). The presence of acceptable collinearity and adequate construct validity were signified by VIF values less than 5. This indicated that an item's contribution to the primary latent construct was unique, as noted by Hair et al. (2021). As shown in Table 4, the VIF values for all items in this study ranged from 1.02 to 1.25.

Table 4 Formative indicator weights and significance testing results (VIF and significance of outer weights)

According to Hair et al. (2021), an item's relative importance in formative constructs is determined by its outer weight, while its absolute importance to the construct is determined by its outer loading. An item was kept in the measurement model if it had a significant outer weight (p < 0.05), or if its outer loading was higher than 0.5. Items that did not meet these criteria were further evaluated based on the significance of their outer loading. If an item's outer loading was lower than 0.5 and not significant, indicating no absolute importance to the construct, it was ultimately removed from the model. As per these criteria, the items that were retained are shown in Table 4.

The structural relationships

We used PLS–SEM to test our proposed theoretical hypotheses, which included the relationships between NM, AM, ML, and the higher and lower levels of CT. The paths with statistical significance (p < 0.05) are shown in Fig. 2. The results indicated that beliefs about the nature of mathematics positively predicted attitude towards mathematics (β = 0.56, t = 11.22, p < 0.001); attitude towards mathematics positively predicted mathematical literacy (β = 0.48, t = 7.06, p < 0.001); mathematical literacy positively predicted lower level computational thinking (β = 0.42, t = 6.40, p < 0.001) and higher level computational thinking (β = 0.38, t = 5.77); and lower level computational thinking positively predicted higher level computational thinking (β = 0.34, t = 5.61, p < 0.001).

Fig. 2

Structural model results (only significant paths are shown). NM: beliefs about the nature of mathematics; AM: attitude towards mathematics; ML: mathematical literacy; LLCT: lower level CT; HLCT: higher level CT. ***p < 0.001

In addition, as shown in Fig. 2, the f ² effect sizes for significant paths were all larger than 0.15, showing a moderate or large effect according to Cohen’s (1988) suggestion that 0.02, 0.15 and 0.35 indicate small, moderate, and large effects, respectively. It is worth noting that the f ² value of beliefs about the nature of mathematics predicting attitude towards mathematics was 0.45, which showed a large effect on attitude towards mathematics.

The predictive validities of the model were indicated by the coefficient of determination (R²) and predictive relevance (Q²) (see Fig. 2). The endogenous constructs including attitude towards mathematics (R² = 30.95%), mathematical literacy (R² = 18.33%), lower level CT (R² = 20.09%) and higher level CT (R² = 40.06%) present acceptable levels of explained variance (Chin, 1998; Tenenhaus et al., 2005). Moreover, the predictive relevance is evaluated through Stone–Geisser’s Q² test. Q² greater than 0 implies that the model has predictive relevance, whereas a Q² less than 0 suggests that the model lacks predictive relevance (Stone, 1974). Our model shows positive Q² values of the endogenous constructs (see Fig. 2; attitude towards mathematics Q² = 0.216, mathematical literacy Q² = 0.049, lower level CT Q² = 0.053 and higher level CT Q² = 0.136) which suggests that the model has predictive validity.

Mediation

As shown in Table 5, attitude towards mathematics, mathematical literacy and lower level computational thinking played significant mediating roles. Attitude towards mathematics mediated the relationship between beliefs about the nature of mathematics and mathematical literacy (β = 0.269, p < 0.001), while mathematical literacy mediated the relationship between attitude towards mathematics and lower level computational thinking (β = 0.203, p < 0.001), and between attitude towards mathematics and higher level computational thinking (β = 0.181, p < 0.001). In addition, lower level computational thinking mediated the relationship between mathematical literacy and higher level computational thinking (β = 0.142, p < 0.001).

Table 5 Mediation analyses showing the direct, indirect, and total effects for the hypothesized model paths

Analysis showed a serial mediation effect between beliefs about the nature of mathematics and lower level computational thinking through attitude towards mathematics and mathematical literacy (β = 0.113, p < 0.001), and also between beliefs about the nature of mathematics and higher level computational thinking (β = 0.101, p < 0.001). Moreover, there was a serial mediation effect between beliefs about the nature of mathematics and higher level computational thinking through attitude towards mathematics, mathematical literacy, and lower level computational thinking (β = 0.038, p = 0.002). Finally, a serial mediation effect between attitude towards mathematics and higher level computational thinking through mathematical literacy and lower level computational thinking was also shown by the analysis (β = 0.069, p = 0.001).

As there were no significant direct relationships between beliefs about the nature of mathematics and mathematical literacy, the indirect effect for the mediation by attitude towards mathematics was full mediation. Similarly, the indirect effect for the mediation by mathematical literacy was full mediation as well. Because mathematical literacy directly predicted higher level computational thinking, the indirect effect for the mediation by lower level computational thinking was partial mediation.

Discussion and implications

This study proposed a hypothesized model to assess the relationships among beliefs about mathematics learning (beliefs about the nature of mathematics, and attitude towards mathematics), ML, and CT (lower level CT, higher level CT). According to the model analysis, it was confirmed that beliefs about mathematics learning could positively predict ML, and ML could, in turn, positively predict CT. Although the direct relationship between beliefs about mathematics learning and CT was not found in the model, beliefs about mathematics learning could indirectly predict CT through ML, which confirms the mediating role of ML in the proposed model. In addition to the above findings, beliefs about the nature of mathematics were found to positively predict attitude towards mathematics, and lower level CT was also confirmed to positively predict higher level CT. In the following, we will discuss our major findings.

First, it was found that CT was directly predicted by ML, indicating that an increase in students’ ML corresponded to an enhancement in their CT skills. These results resonate with the findings of Durak and Saritepeci (2018) and Özgür (2020). Wing’s (2008) comments indicating that CT is a concept that integrates mathematical thinking into solving a problem, designing and evaluating a system, and understanding intelligence and human behavior support this finding in this research. Similarly, Alyahya and Alotaibi's (2019) discovery of a significantly positive correlation between CT and TIMSS mathematics achievements aligns with our findings. In addition, the outcomes from Román-González et al. (2018b) affirm that CT serves as a crucial indicator for estimating mathematics achievement, further reinforcing our study's outcomes.

Moreover, the findings indicated that students’ beliefs about mathematics could positively predict ML. Besides the positive correlation between beliefs about mathematics and ML, the increase in students’ beliefs about mathematics could positively increase their ML. Moreover, the results showed that beliefs about the nature of mathematics as part of beliefs about mathematics positively predicted the other subscale—attitude towards mathematics, which indicates that the stronger students’ thoughts about the value of mathematics, the higher their confidence in learning mathematics. A past study found that beliefs about the nature of mathematics was positively correlated with attitude towards mathematics (Kaldo & Hannula, 2014), and this study provides further indication of the direction of the predictive relationship. Nevertheless, beliefs about the nature of mathematics only indirectly predicted ML through attitude towards mathematics. This outcome might be attributed to the abstract nature of beliefs about the nature of mathematics for junior high school students. In this stage of learning, students’ attitude towards mathematics plays a pivotal role in predicting their mathematical literacy. Future studies could explore whether older students, such as high school or post-secondary students, possess a better grasp of these abstract concepts.

Finally, our findings revealed that beliefs about mathematics positively predicted CT, albeit through the intermediary of ML. In essence, enhancing students' perceptions of mathematics and its significance in life not only boosts their confidence in learning mathematics but also augments their real-life problem-solving abilities. While previous studies primarily focused on the relationship between pairs of constructs, our results extend this examination to encompass the relationships among all three constructs.

There are two implications of teaching mathematics and CT. This study demonstrated the importance of students’ beliefs about mathematics and ML in predicting CT competence. Therefore, to promote CT competencies, in addition to providing more learning opportunities for CT, improving students’ understanding of mathematics may be beneficial. Specifically, researchers and teachers should pay more attention to students’ beliefs about mathematics in addition to promoting their mathematical literacy. Some researchers have suggested that students’ beliefs about mathematics depend on their mathematics learning experiences and their view of mathematics (Lazim et al, 2004). One approach to enhancing students’ mathematical literacy and providing meaningful mathematics learning experiences is through integrating real-life situations into mathematics learning (Barcelos et al., 2018; Cui et al., 2023). Designing a mathematics curriculum based on topics relevant to students’ daily life experiences may help students develop mathematical literacy and views of mathematics (Amirali, 2010), which, in turn, can help them develop CT competencies.

Second, we suggest integrating the teaching of CT with mathematics, such as designing STEM (science, technology, engineering, and mathematics) -oriented activities or curricula (Zhang et al., 2023). Recently, the trend of incorporating CT into interdisciplinary education, particularly within STEM domains, has been noted (Lee et al., 2020; Li et al., 2020a). In addition to gaining knowledge and skills, students can develop multi-dimensional and multidisciplinary competence through integration (Dolgopolovas & Dagienė, 2021). Studies have also shown the benefit of STEM content for CT learning (Bortz et al., 2020). Studies have implemented problem-based instruction, games, or robots in the STEM curriculum for students of various ages and for pre-service teachers as well (Wang et al., 2021; Wawan et al., 2022). Examples include using Scratch (Rodríguez-Martínez et al., 2020) or the integrated 6E Learning by DeSIGN™ Instructional Model (i.e., engage, explore, explain, engineer, enrich, evaluate) with LEGO robots to improve students’ CT (Chiang et al., 2022), and designing an engineering-based activity at a STEM camp (Shang et al., 2023). There are also studies that have implemented innovative teaching methods in the curriculum, such as integrating CT into mathematics education through programming role-playing or embodiment (Sung et al., 2017).

Finally, the findings of this study also have some methodological implications. First, while most of the studies treated the CT scale or CT assessment as a reflective construct (e.g., Korkmaz et al., 2017), in this study, CT was treated as a formative construct. Researchers have also suggested the importance of carefully considering the nature of the items and making informed decisions regarding whether to treat the measurement as formative or reflective to prevent model mis-specification (Lin et al., 2020). Second, based on Tsai et al. (2022), this study confirmed that CT could be divided into lower level (abstraction, decomposition) and higher level (algorithmic thinking, evaluation, and generalization), where lower level CT could positively predict higher level CT. The results of categorization in the previous study were based on CT disposition, and this study used assessment data to further verify the two-level structure of the constructs. Future studies should consider CT as a two-level rather than a one-level construct.

While this study contributes insights into the relationships between mathematics learning and computational thinking, it has some limitations that should be acknowledged. One limitation is the sample size and the age of the students. Due to the time needed to complete the survey and tests, we were only able to recruit a limited number of participants, which may not fully represent the diverse range of learners. In addition, our sample was limited to students at the junior high school level. The relationships between mathematics learning and computational thinking may change due to, for instance, students’ mastery of abstract thinking. Another limitation of the educational study is the exclusion of heuristic and meta-cognitive aspects of mathematics learning, such as the monitoring and control of problem-solving strategies (Schoenfeld, 1992). Furthermore, this study failed to account for personal attributes, such as self-efficacy, persistence, and creativity (Rozgonjuk et al., 2020). Neglecting these factors may hinder a comprehensive understanding of the multifaceted nature of mathematics learning. Incorporating these aspects into future research could provide a more holistic perspective on the relationships between mathematics learning and CT.

Conclusions

In this study, we proposed a model suggesting the relationships between students’ understanding of mathematics and CT. The model highlights the roles of mathematical literacy (ML) in both directly predicting CT competence and mediating the relationships between beliefs about mathematics and CT. Therefore, we suggest enhancing students’ mathematical literacy or integrating mathematics and CT into the same learning activities to promote CT competence. Another interesting finding is that attitude towards mathematics directly predicted students’ ML and also mediated the relationships between beliefs about the nature of mathematics and ML. The results indicate that students’ attitude towards mathematics may be a more important predictor than their beliefs about the nature of mathematics, at least for students at this stage. Finally, we recommend that future studies consider CT as a two-level construct and treat CT tests as a formative rather than a reflective construct.

Appendices

Appendices

Appendix 1

A sample item from CTT–JH

There are various agricultural products on Jack’s Happy Farm. To distinguish different items, Jack developed a method called Quick Jack Code (referred to as QJ-code). It is a code made up of squares, each of which represents a certain value. The squares were filled row by row from bottom to top and from right to left. Starting with 1 from the bottom right square, the value of the other squares is twice the value of the previous one.

For example, this is a 3 × 3 QJ-code. Jack darkens some squares to encode numbers. The coded number is the sum of the values of all the dark squares, so the coded number in this QJ-code is 2 + 32 + 64 = 98.

Which of the following 4 × 4 QJ-codes represents the largest coded number?

Appendix 2

The corresponding CT constructs assessed by the CT test items

Level	Item	Abstraction	Decomposition	Algorithm	Evaluation	Generalization
L	Q1	V			#
L	Q2	V	V
L	Q3		V
L	Q4	V	V			#
H	Q5	#			V	V
H	Q6			V		V
H	Q7			V		V
H	Q8				V	V

H: higher level; L: lower level; V: primary construct; #: secondary construct

Appendix 3

Sample items of the Mathematics Literacy Test

Q1. Ferris wheel

A giant Ferris wheel is on the bank of a river. See the picture and diagram below.

The Ferris wheel has an external diameter of 140 m and its highest point is 150 m above the bed of the river. It rotates in the direction shown by the arrows.

Translation note: in this unit, please retain metric units throughout

Q1-1: Ferris wheel (PM934Q01, Employ)

• The letter M in the diagram indicates the centre of the wheel.

• How many metres (m) above the bed of the river is point M?

Answer: _______________ m.

Q1-2: Ferris wheel (PM934Q02, Formulate)

• The Ferris wheel rotates at a constant speed. The wheel makes one full rotation in exactly 40 min.

• John starts his ride on the Ferris wheel at the boarding point, P.

• Where will John be after half an hour?

• A. At R.

• B. Between R and S.

• C. At S.

• D. Between S and P.

Q2. GARAGE

• A garage manufacturer’s “basic” range includes models with just one window and one door.

• George chooses the following model from the "basic" range. The position of the window and the door are shown here.

  

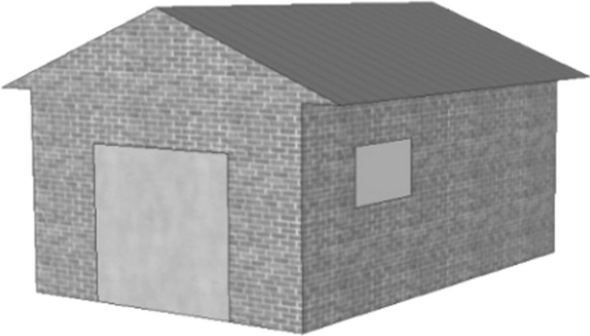
Q: GARAGE (PM991Q01, Interpret)

• The illustrations below show different “basic” models as viewed from the back. Only one of these illustrations matches the model above chosen by George.

• Which model did George choose? Circle A, B, C or D.